Engineering as Shadow Price Discovery

Engineering: solving problems under constraints

Many engineering problems have the general form of trying to achieve some desired capabilities at minimum cost, or alternatively trying to design the best performing system within a certain price point. For purposes of a concrete example, say we are designing one of those rolling delivery robots like these ones I used to see rolling around Redwood City, California. To simplify, say that we need to achieve some range target while keeping the size below a certain city-mandated limit, and we’d like to have as much cargo capacity as possible while minimizing costs.

Tackling this problem, we realize that a cheaper battery can get us the desired range, but takes up more room that could otherwise be used for cargo capacity. More cargo capacity means more weight which requires more battery power for the same range. Everything costs money. How to decide what to do?

There are always trade-offs / No Free Lunch

Besides being something nice to say in a meeting if you have nothing else to add to the discussion, what does it mean to say that “there are always trade-offs”? Consider the case where this is not true: ie, you can potentially increase something good (performance, reliability, capacity) or decrease something bad (cost, pollution, delays) in the design without paying any price along other dimensions. This is sometimes known as a “free lunch”, and of course you would take it. Now, having maxed out on all available free lunches, you are now at some point in the constraint space where you can no longer get something for nothing. Once again, there are trade-offs! This is why there are always trade-offs: if there were free lunches to be had you would have already taken them, so here you are facing trade-offs.

Constrained Optimization

Constrained Optimization gives us a formal way to define problems where we want to maximize (or minimize) some mathematical function \(f(x)\) (known as the objective function) in terms of variables \(x\) which are subject to some constraints (either equality \(g(x)=c\) or inequality \(h(x) \leq d\)) that define the feasible set of possible solutions. This field and its associated literature are vast and fascinating, and the amount of real-world activity influenced or controlled by the solutions of these optimizations is mind-boggling. In some sense, the tools of optimization can give us a rigorous way to navigate trade-offs.

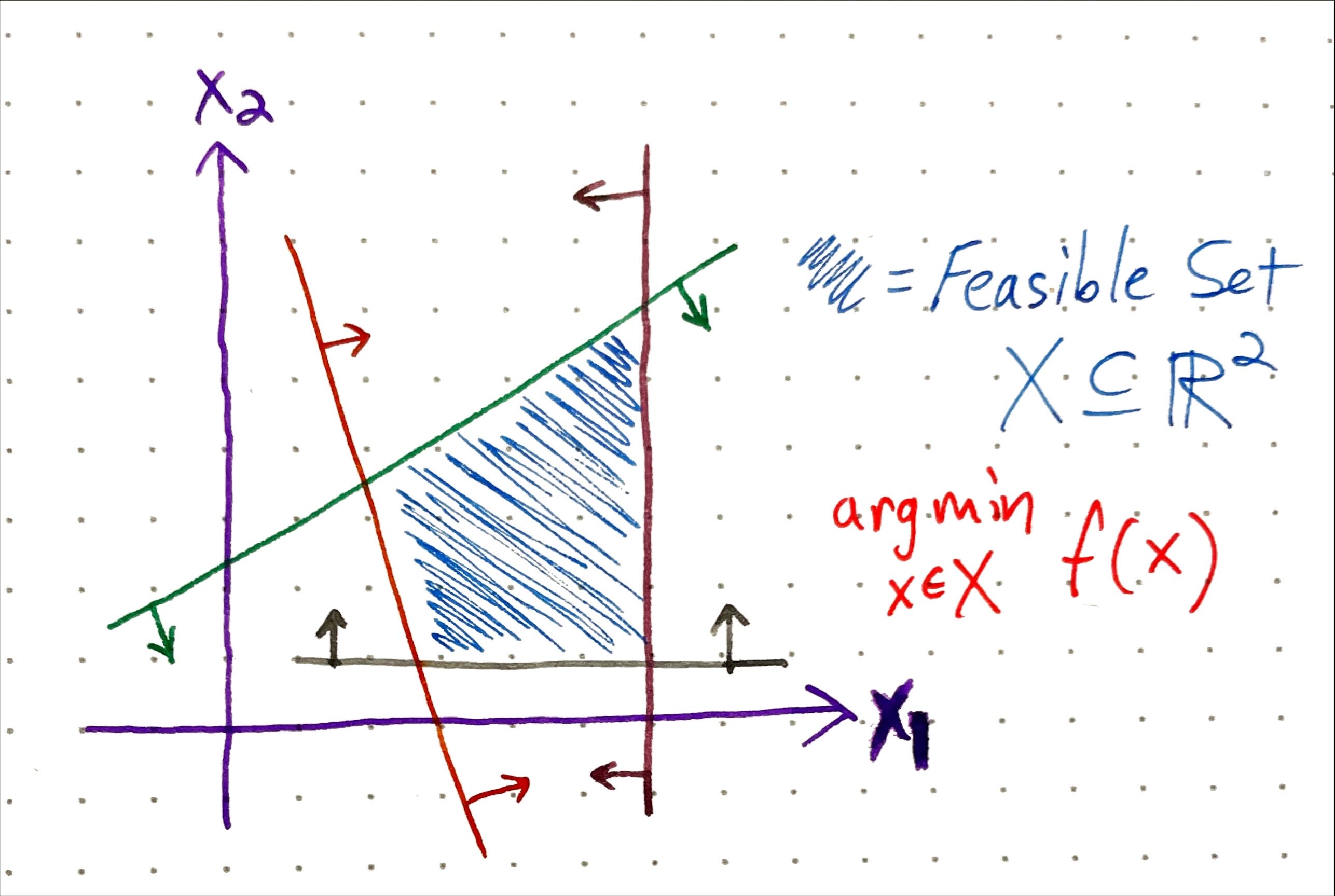
We are just employing these concepts in an intuitive hand-wavy way here and we won’t be digging too deeply into actual equations. Going back to our delivery robot, imagine that we can drop in some specific objective function and parameters to perfectly capture the constraints and optimization goal described above. In this scenario, we can then just drop all this into some solver software and magically get the quantitative parameters that define the optimal or ideal design - hooray!

Shadow Prices

Having designed the perfect cargo robot for your exact circumstances, you are enjoying a coffee when your Product Manager (PM) bursts into the room and informs you that your employer has successfully lobbied to have local regulations changed to increase the maximum size of cargo robots by 3.7%! What does it mean for your design?

Before tackling this question, we must circle back to the original objective function definition. Recall that we want “as much cargo capacity as possible while also minimizing costs.” Unfortunately this is not, strictly speaking, a coherent objective function as we’ve no way to weigh a gain in cargo space against a decrease in costs. Instead, we have to define some “profitability” objective to be maximized that goes up with cargo space and down with manufacturing costs. In this definition, our stakeholders (say, the aforementioned PM) must have devised a valuation model for cargo space that standardizes its unit of measure to be directly comparable to manufacturing costs - eg, $10 per cubic meter of storage.

Shadow Prices extend this standardization to all of the other variables and constraints. At a given optimal solution, the shadow price for a given constraint tell us how much “better” we could do on the objective function (eg, profitability) if this constraint were very slightly (ie, infinitesimaly) relaxed. This means that, given the shadow price of the “size” constraint at our solution, we can now calculate the the approximate ROI of our company lobbyist who negotiated that 3.7% increase - great job!

Shadow Price discovery

In our cargo robot example, things worked out very nicely that the objective function was a relatively unambiguous target like “money”, and also that the PM was somehow able to devise a closed-form cash valuation model for cubic meters of cargo space. In real-world projects thing may not work out so cleanly. In fact, for an internal software engineering project, it is likely that there is not a well-defined objective function in the exact same sense as in our toy robot example. Instead, we may have a “multi-dimensional” objective with unclear weightings among the desired properties or capabilities:

• speed of delivery: when can we have it by?
• maintainability or extensibility of the code
• cost (in AWS bills) to operate
• reliability (uptime) of the component
• various “nice-to-have” features or capabilities

We are now far afield of the well-defined world of Constrained Optimization, but perhaps we can lean on some of the intuitions we developed? Unfortunately, it may be incredibly difficult or even impossible to come up with sensible weightings between these properties. How much uptime are we willing to pay in order to get the component 1 sprint earlier? What is the cash value of refactoring the code to allow for easier extension in the future? Your stakeholders are not going to grind out an \(N^2\) matrix of conversions weights between the various dimensions. How can we discover the appropriate shadow prices or exchange rates among the different properties of our solutions in order to choose the appropriate trade-offs?

Pricing with assortments

Harrison Metal has some nice short videos explaining various business-related concepts. Several of them explicitly target pricing, and in particular one of them covers the idea of assortments.

The video describes how vertical (good, better, best) and horizontal (different in kind) product assortments (along with optional “add-ons”) can be used to probe the marketplace and capture demand (more details in slides). What I find particularly interesting here is pricing as discovery: the variation supplied by the assortments “explores” the local neighborhood of latent consumer demand and reveals valuable information about who is willing to pay how much for what.

Now we come to an interesting idea: while stakeholders may not be willing or even able to explicitly articulate an \(N \times N\) exchange rate matrix among wildly varying (and potentially discontinuous or lumpy) trade-offs in a design or plan, they are more likely to be able to choose or rank alternatives among a finite assortment of candidate proposals that vary along the relevant dimensions, thereby implicitly expressing some weightings among the crucial trade-offs.

Returning to our cargo robot, let’s pretend we do not have all of the nice equations and parameters we had previously assumed. Instead, we can propose three alternatives to the PM:

1. “econo-bot” that goes all-out to minimize cost but has less cargo space
2. “deluxe” design that has maximum cargo space, but at greater cost
3. some medium tradeoff that interpolates between 1. and 2.

Based on the feedback we get among these proposals, we gain some idea where the PM (our internal customer) believes the “sweet spot” to be is in terms of trading off cost and cargo space - hooray again!

Back to reality

Let’s try to fit this hypothetical scenario into some coherent framework of problem-solving in engineering. We can define “inner-loop” engineering as finding the best (or good enough) solution given a very nicely defined problem in terms of the goal and constraints. This is often no simple business, for “nature cannot be fooled”¹ as they say. But (certainly in software, probably everywhere) even this challenge is often embedded in an “outer-loop” problem of identifying and carefully defining the appropriate goal(s) and constraints in the first place. Given that this outer-loop defines the boundary between the “pure” technical solution and the messy human world, it is often a complex affair that, like pricing, can be more art than science. This is often where the trade-offs get traded-off, and hopefully these ideas from constrained optimization and pricing can help provide a useful conceptual toolkit for navigating these situations.

Finally some caveat: in a previous post I described a mental model of product development sequencing based on Prize-Collecting Steiner Trees (PCST), a famous combinatorial optimization problem in theoretical computer science. I thought it was a useful conceptual framework, but I also cautioned against trying to literally encode your problems in that way. Likewise, here I would not recommend actually trying to infer shadow prices or compute the NPV of a given bugfix, but it might be useful keep these tools and ideas in mind when trying to navigate tricky trade-offs among difficult-to-compare dimensions, and consider how one might implicitly elicit relative valuation information from stakeholders and/or domain experts via the presentation of carefully constructed alternatives.

Written on October 30th, 2022 by David M. Andrzejewski